 |
|
 |
 |
| Les trois médianes d'un triangle sont concourantes en
un point,
appelé centre de gravité du triangle , et noté
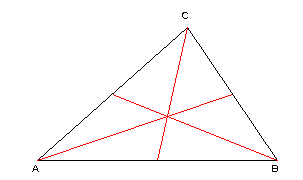
habituellement G. Référence bibliographique : Mathématique 4e, Hachette Collège, p 215. |
|
 |
|
| Si un point est le point de concours des médianes d'un triangle alors ce point est le centre de gravité du triangle. | Si un point est le centre de gravité d'un triangle alors toute médiane de ce triangle passe par ce point. |
 |
|
| Le centre de gravité se trouve aux deux
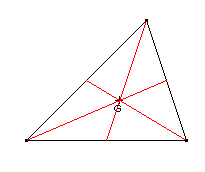
tiers de chaque médiane, à partir du sommet correspondant. Référence bibliographique : Mathématique 4e, Magnard, p 130 |
Le centre de gravité d'un triangle
est sur chaque segment de médiane limite par un sommet et le milieu du coté opposé, au tiers de la
longueur à partir du coté . Référence bibliographique : Mathématiques 4e Technologique, Hachette Technique, 1990, p118 . |
 |
|
| Construction
d'n triangle ABC avec : AB = 5cm AC = 4cm BC = 6cm . Construction des médianes puis du centre de gravité. |
|
 |
|
| Dupont Marjorie | |
 |
|||
| Pas de rubrique associée | |||
