 |
|
 |
 |
| Dire que A'
est le symétrique de A par rapport à (d), c'est dire
que (d) est la médiatrice de [AA']. Référence bibliographique : Connaître et pratiquer les mathématiques, 6e, Nathan, 1986, p. 133. |
|
 |
|
| Si A' est le symétrique de A par rapport à (d) alors (d) est la médiatrice de [AA']. | Si (d) est la médiatrice de [AA'] alors A' est le symétrique de A par rapport à (d). |
 |
|
| -
A' est le symétrique du point A par rapport à à la
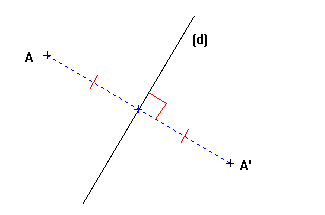
droite D. - La droite D est la médiatrice du segment [AA']. - Seuls les points de la droite D sont égaux à leur symétrique. Référence bibliographique : Mathématiques 6e, collection Pythagore, Hatier, 1986, p. 150. |
Dire
que deux points distincts A et B sont symétriques par
rapport à une droite D, c'est dire que D est la médiatrice de [AB]. Référence bibliographique : Maths 6e, collection Alpha, Hatier, 1994, p. 179. |
 |
|
| Têtu Mickaël | |
| Hurbain Thomas | |
 |
|||
| Pas de rubrique associée | |||
