G:\GéoWeb_\commun\pages\corps.html



Deux points distincts A et B sont symétriques par rapport à un point O lorsque O est le milieu du segment [AB]. Référence bibliographique : Math 5ème, Belin, 1995, p 144.

Si A et B sont symétriques par rapport à un point O alors O est le milieu du segment [AB].	Si O est le milieu d'un segment [AB] alors A et B sont symétriques par rapport au point O.

Le point O est centre de symétrie d'une figure si, par demi-tour autour de O, cette figure coïncide avec elle-même. Référence bibliographique : Mathématiques 5ème, Bordas, 1991, p 62.	Correspondance point à point de deux figures, telles que les points correspondants de l'une et de l'autre soient à égale distance de part et d'autre d'un point. Référence bibliographique : Dictionnaire Hachette, 1994.

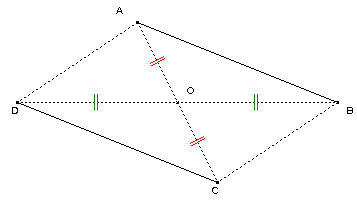
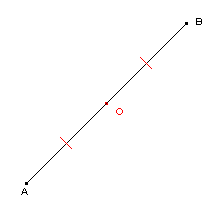
Soit un segment [AB] et O un point quelconque en dehors du segment [AB]. Construire C symétrique de A par rapport à O et D symétrique de B par rapport à O. Que peut-on dire du quadrilatère ABCD ? A et C sont symétriques par rapport à O donc O est le de milieu [AC]. B et D sont symétriques par rapport à O donc O est le milieu de [BD]. Les diagonales du quadrilatère ABCD se coupent en leur milieu O. Ce quadrilatère est donc un parallélogramme.

Marlard Catherine