
Référence bibliographique : Mathématiques 4e, Tout simplement, Hachette, 1998, p.25.
Référence bibliographique : Mathématiques Collège, Istra, 1998, p. 140.
Référence bibliographique : Mathématiques 4e, Nathan, 1993, p. 142.
 |
|
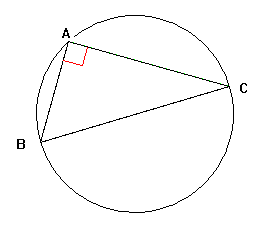
| Le cercle
circonscrit à un triangle
rectangle a pour
diamètre l'hypoténuse de ce triangle. Référence bibliographique : Mathématiques 4e, Tout simplement, Hachette, 1998, p.25. |
|
| Si un cercle est circonscrit à un triangle rectangle alors il a pour diamètre l'hypoténuse de ce triangle. | Si un cercle a pour diamètre l'hypoténuse d'un triangle rectangle alors ce cercle est circonscrit au triangle. |
| Le centre du cercle
circonscrit
à un triangle rectangle est le milieu de l'hypoténuse. Référence bibliographique : Mathématiques Collège, Istra, 1998, p. 140. |
Dans un triangle
rectangle, le cercle
circonscrit au
triangle a pour diamètre l'hypoténuse. Référence bibliographique : Mathématiques 4e, Nathan, 1993, p. 142. |
| Dulieu Céline | |
| Houliez Nathalie | |
| Pas de rubrique associée | |||