Dans cette page, nous proposons quelques démarches de recherche intéressantes relevées parmi les productions des élèves de sixième. Ces démarches ne sont pas toutes finalisées mais montrent la diversité des heuristiques* échafaudées par ces élèves.

*heuristique : démarche de recherche

Défi n°1

• Compter de 9 en 9 à partir de 1905.
  1905, 1905 + 9 = 1914, 1914 + 9 = 1919 etc.

• Recherche exhaustive avec calcul pour chaque année de 1901 à 1977  (abandon pour les années suivantes...) : 1+9+0+1 = 11, 1+9+0+2 = 12, 1+9+0+3 = 13, 1+9+0+ 4 = 14, 1+9+0+5 = 15, etc.

• Séparation mise en évidence entre les 2 premiers et les 2 derniers chiffres des dates. Démarche insuffisamment ordonnée qui n'a pas permis de trouver toutes les réponses attendues :
  1 + 9 + 3 + 2 = 15, 1 + 9 + 4 + 1 = 15, 1 + 9 + 5 + 0 = 15, 1 + 9 + 2 + 3 = 15,
  1 + 9 + 1 + 4 = 15, 1 + 9 + 0 + 5 = 15
   

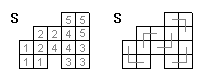
Défi n°4

• Pavage matérialisé soit par des chiffres, soit par des traits  

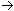
 Défi n°7

• Comptage des déplacements par regroupement de 10 en 10 jusqu'à 120 : 10 C* ; 20 C ; 30 C ; ... ; 120 C
  puis un par un : 121   I ; 122   C ; 123 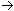I ; ... ; 127  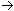 I
  * : erreur initiale mais la démarche est juste.

• Représentation spatiale en colonne  du nombre de trajets effectués, ce qui met en évidence l'intérêt de la notion de parité pour la résolution du défi :

Matérialisation des points d'arrivées sous forme schématique avec regroupement pour dénombrement :

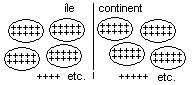
Défi n°9

• Dénombrement des cubes avec 1, 2 ou 3 gommettes (24 + 24 + 8). Calcul de la différenceentre le nombre total de cubes (64) et le nombre de cubes avec gommettes (56*) pour trouver le nombre de cubes sans gommettes : 64 - 56 = 8
  * En réalité, les élèves ont commis une erreur de calcul et donné comme total 54 au lieu de 56 mais la démarche utilisée est pertinente.

 Défi n°10

• Méthode 1 avec mesures (approchées !) et calcul des chemins parcourus
  pour Cargo : 6,4 horiz. + 4,2 vert. 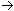10,6
  pour Escar : 1,6 x 4 horiz. + 1 x 4 vert. 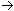 10,4, d'où la réponse erronée proposée : Escar !
• Méthode 2 avec mesures (à nouveau approchées !) et calcul des chemins parcourus
  pour Cargo : 6,4 horiz. + 4,3 vert. 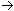10,7
  pour Escar : 1,6 + 1 + 1+ 1,6 + 1 + 1,6 + 1 + 1,6 + 1 = 10,4 d'où la réponse erronée proposée : Escar !
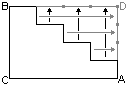
• Méthode 3 avec raisonnement géométrique schématisé : mise en évidence de longueurs égales entre le parcours d'Escar (marches de l'escalier) et le parcours virtuel A-D-B, d'où la réponse juste : arrivée simultanée d'Escar et Cargo.

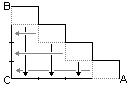
• Méthode 4 avec raisonnement géométrique schématisé : mise en évidence de longueurs égales entre un escalier virtuel (représenté en pointillés) et le parcours de Cargo (A-C-B), d'où la réponse à nouveau juste : arrivée simultanée d'Escar et Cargo.

  présentation | éléments statistiques